Cito rekenen: kommagetallen
Kommagetallen
Dagelijks merk ik dat leerlingen moeite blijven houden met kommagetallen, en zeker met het omrekenen van kommagetallen naar breuken of procenten. In en vorige post ging het ook over kommagetallen, maar dan voornamelijk het vermenigvuldigen en delen ervan. Optellen en aftrekken is natuurlijk ook belangrijk, dus bij deze even een extra uitleg over kommagetallen:
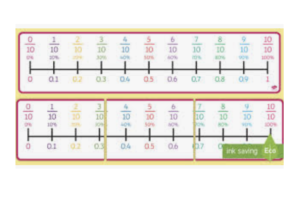
Allereerst, jullie kennen allemaal dit schema: E, t h,d. De E staat voor eenheden (de getallen 0 tot en met 9); de t staat voor tienden (0,6 betekent dus 6 tienden of 6/10); de h staat voor honderdsten (0,23 betekent dus 23 honderdsten of 23/100); de d staat voor duizendsten ( 0,087 betekent dus 87 duizendsten of 87/1000)
Schrijf 0,7 als een breuk. Schrijf 0,023 als een breuk. Schrijf 0,85 als een breuk. Hoe werkt dat?
0,7 –> er staat één getal na de komma, dus het zijn tienden –> 6/10. In procenten: 6/10 = 60/100 = 60%
0,023 –> er staan drie getallen na de komma, dus het zijn duizendsten –> 23/1000. In procenten: 23/1000 = 2,3/100 = 2,3%
0,85 –> er staan twee getallen na de komma, dus het zijn honderdsten –> 85/100. In procenten: 85/100 = 85%
Optellen of aftrekken van kommagetallen
0,2 + 0,15 = ?
Tel je de 2 (van 0,2) op bij de 1 of bij de 5 van 0,15? Het antwoord is 0,35, want tienden tel je op bij tienden: 0,2 zijn twee tienden en 0,15 bestaat uit één tiende en 5 honderdsten. Een tip: als je kommagetallen bij elkaar optelt (of van elkaar aftrekt) zorg er dan voor dat er achter de komma even veel getallen staan. Pas de getallen dus aan:
0,2 + 0,15 = 0,20 + 0,15 = 0,35
En zo ook:
0,65 + 0,3 = 0,65 + 0,30 = 0,95
1,041 + 0,6 = 1,041 + 0,600 = 1,641
2,5 – 1,055 = 2,500 – 1,055 = 1,445
Vermenigvuldigen van kommagetallen
0,6 x 0,02 = ?
Tip: vermenigvuldig eerst de getallen (6 x 2 = 12), tel dan het totaal aantal plekken ná de komma (0,6 heeft één kommaplaats en 0,02 heeft twee plaatsen na de komma, in totaal dus drie kommaplaatsen). Zet bij het antwoord 12 nu de komma drie plaatsen terug: 12 wordt dan 0,012.
En zo ook:
0,5 x 0,3 = 0,15 (5 x 3 = 15 en dan de komma twee terugzetten )
0,12 x 0,5 = 0,06 (12 x 5 = 60 en dan de komma drie plaatsen terugzetten)
Delen met kommagetallen
6 : 0,2 = ?
Delen betekent: hoe vaak past het tweede getal in het eerste getal. De vraag bij deze som is dus: hoe vaak past 0,2 in 6? Eerst een andere vraag: hoe vaak past 0,2 in 1 (of: hoe vaak past € 0,20 in € 1,00, want 0,2 is natuurlijk hetzelfde als 20 cent). Het antwoord is 5 keer. Als 0,2 vijf keer in 1 hele past, dan past 0,2 in 6 helen 30 keer. 6 : 0,2 = 30
Tip: als je bij een deelsom beide getallen vermenigvuldigt met hetzelfde getal, dan blijft de som gelijk. 8 : 2 is dus hetzelfde als 16 : 4 (beide getallen met 2 vermenigvuldigd) of als 40 : 10 (zowel de 8 als de 2 met 5 vermenigvuldigd). Bij 6 : 0,2 kan dit natuurlijk ook: vermenigvuldig beide getallen met 10 –> 6 : 0,2 wordt dan 60 : 2 =30. Of, beide getallen vermenigvuldigen met 5 –> 6 : 0,2 wordt dan 30 : 1 = 30
En zo ook:
5 : 0,25 = 20 : 1 = 20 (beide getallen vermenigvuldigen met 4) 0f 500 : 25 = 20 (beide getallen vermenigvuldigen met 100)
60 : 1,5 = 120 : 3 = 40 (beide getallen vermenigvuldigen met 2) of 600 : 15 = 40 (beide getallen vermenigvuldigen met 10)
Als het goed is, begrijp je nu beter hoe je kunt rekenen met kommagetallen. Mocht iets nog onduidelijk zijn, laat een berichtje achter!
Wil je een uitgebreide uitleg over alle Cito rekenonderdelen? Bestel dan een Cito Oefenboek. In deze Oefenboeken staat ook een uitgebreide uitleg bij alle andere onderdelen van de Cito-toetsen, zoals begrijpend lezen, taal en spelling.
